| │サイトマップ│Japanese│English│ |
-
進学希望者の方へ
-
研究内容
- 物質の変化を計算科学する
- 非平衡系
- 凝集系化学反応
- マクロ化学現象
- 生命現象
- マルチスケール情報処理
- 産業応用
- 2023年度
- 2022年度
- 2021年度
- 2020年度
- 2019年度
- 2018年度
- 2017年度
- 2016年度
- 2015年度
- 2014年度
- 2013年度
- 2012年度
- 2011年度
- 2010年度
- 2009年度
- 2008年度
- 2007年度
- 2006年度
- 2005年度
- 2004年度
- 2003年度まで
- 2000年度まで
- 2019年度
- 2018年度
- 2017年度
- 2016年度
- 2015年度
- 2014年度
- 2013年度
- 2012年度
- 2011年度
- 2010年度
- 2009年度
- 2008年度
- 2007年度
- 2004〜2006年度
- 2003年度
コンセプト研究内容学会・セミナー
オープンセミナー
参考文献
設備
-
メンバー
- スタッフ
- 研究生・学生
- OB・OG
- OB・OGの声
- 2018年度〜
- 2015〜2017年度
- 1999〜2014年度
メンバーアルバム -
アクセス
- アクセスマップ
- 東山キャンパスマップ
- 風景(外観)
- 書類宛先
- 受験案内 ※リンク
アクセス住所 -
関連サイト
分子運動から非平衡系へ
自然界で起こる様々な非定常非平衡現象を、フォッカー−プランク方程式による物質の濃度変化の取り扱いと分子動力学(MD)シミュレーションを併用し、マクロとミクロな視点からその非平衡性の起源を理論的に明らかにすることを目的としている。
凝集化学反応系に関する粗視化方程式について
凝集系は通常アボガドロ数個の分子を含む統計集団として扱われる。この系を厳密に扱うためには古典的にはアボガドロ数個のニュートン方程式を並列計算する必要がある。しかしながら、このような超多自由度系はどんな計算機を用いても実現不可能であるため、可能な粗視化が必要とされる。
クラマースによって反応座標系における確率的運動方程式(ランジュバン形式やフォッカー−プランク形式)が提供されている。この表式では溶質の運動に比べて溶媒の運動が十分速いことを仮定しているが、そのような仮定は実際には成立していない。この問題を修正するために、森らは分離の難しい複数の時間スケールに関する問題を扱うために一般化した。我々は化学反応系に着目し、溶媒分子を媒介した反応分子内モード間カップリングの重要性を示した。
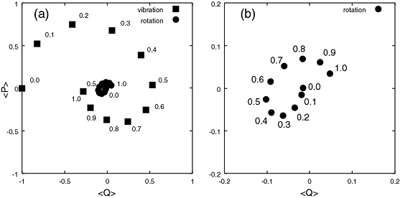
図2 モード間カップリングによる回転モードの誘起
MDシミュレーションによる統計解析について
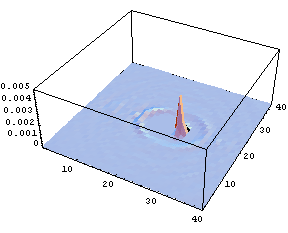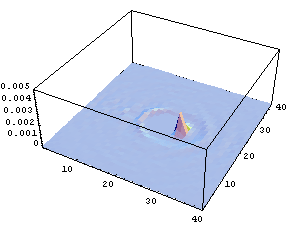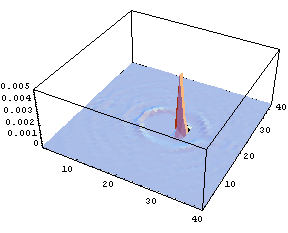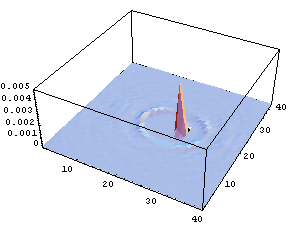
図3 酸素原子の数密度分布
溶質分子内自由度だけで凝集系化学反応を表現することが不可能であることは、溶媒分子もまた分子内自由度を持ち、その結果溶媒分子が溶質分子の周囲で構造化していることから明らかである。実際に起きている現象を確認するためにMDシミュレーションを利用することは有用である。平衡状態にある異核二原子分子を振動励起し、その後の溶液の変化を記録した物が次の図である。統計的集団として捉えるために、多数回のシミュレーション結果を統計平均して可視化した。
局所運動エネルギーや局所パワースペクトルに関する時系列解析の結果、異核二原子分子の非対称性のためにエネルギー伝搬も非対称に現れることや、溶媒分子の振動励起・緩和過程や溶媒和構造の揺らぎが溶媒分子内・溶媒分子間の振動カップリングに関連していることが判明した。
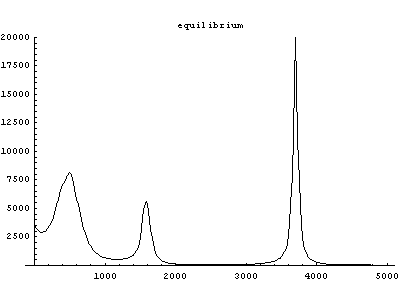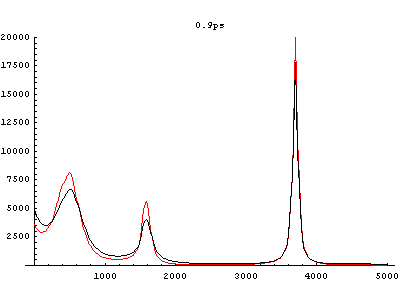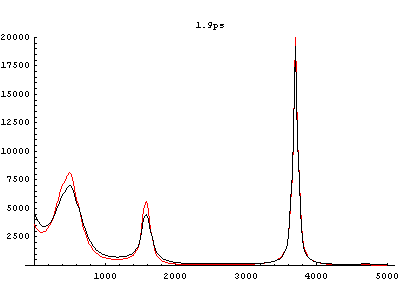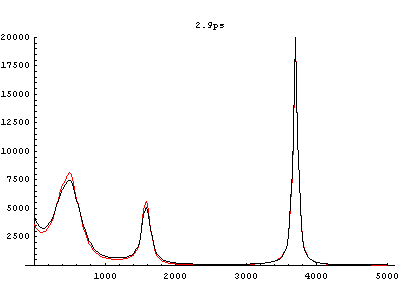
図4 異核二原子分子周囲の溶媒和水分子集団に関するスペクトル。(赤:平衡系、黒:振動励起系)
摂動アンサンブルMD法による緩和過程の統計的解析
平衡状態にある凝集系の溶質分子を振動励起して統計平均(集団(アンサンブル)平均)すると、溶質分子の緩和過程を解析可能であることを示した(上記研究)。この操作に摂動的な取り扱いを付け加えた摂動アンサンブルMD法を用いることで、より高い精度で緩和過程の特徴を解析することが可能となる。この手法では、平衡状態に局所的に摂動を与えることで生まれる非平衡状態での“摂動MD(Perturbed MD, PMD)シミュレーション”と、平衡状態のまま実行する“非摂動MD(Unperturbed MD, UMD)シミュレーション”の組を、ある時刻、空間領域において必要となる観測量の分解能に応じて決まる回数だけ実行して、対応する統計平均を求める。
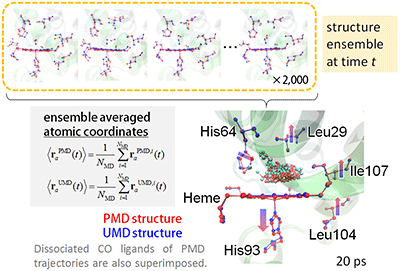
図5 一酸化炭素結合型ミオグロビンのCOリガンド光解離後に生じる構造変形(摂動アンサンブルMD法により解析して得られた結果)。赤色の構造は摂動MD(Perturbed MD, PMD)計算、青色の構造は非摂動MD(Unperturbed MD, UMD)計算の構造。
図5に摂動アンサンブルMD法を一酸化炭素(CO)結合型ミオグロビンのCOリガンド光解離過程の解析に適用した結果を示す。同一の初期構造からリガンドCOを解離させたPMDと、解離させず平衡状態のまま実行するUMDの組を、異なる2000個の初期構造に対して実行した。時刻t = 20 psにおける構造アンサンブルに対して統計平均することで、CO解離後のミオグロビンが示す、過渡的な平均的な構造変形を得ることができ、時間分解X線結晶回折測定により得られている構造変形をよく再現した。さらに、光吸収により生じる熱せられたヘムから、ミオグロビンのヘム近傍アミノ酸残基への振動緩和経路の解析にも成功した。
【参考文献】
1. M. Takayanagi, H. Okumura, M. Nagaoka, J. Phys. Chem. B, 111, 864 (2007).
2. M. Takayanagi, C. Iwahashi, M. Nagaoka, J. Phys. Chem. B, 114, 12340 (2010).
3. M. Takayanagi and M. Nagaoka, Theoret. Chem. Acc., 130, 1115 (2011).
4. M. Nagaoka, I. Yu, M. Takayanagi, in "Proteins: Energy, Heat and Signal Flow" (CRC Press) (Eds., D.M. Leitner, J.E. Straub)
統計集団
或る統計的集団におけるデータセットについての平均。統計力学においては集団(あるいはアンサンブル)平均を意味することが多く、時間変化するデータセットについての平均である時間平均とは区別して用いられる。本来は可能な全ての状態に関する集団平均でなければならないが、実用上、与えられたデータセットに関する平均値を推定値として用いる。
摂動アンサンブルMD法
平衡状態における初期構造から、局所的な摂動を与えた摂動MD(PMD)と、非摂動MD(UMD)の組を実行し比較する摂動的なアプローチは、摂動によって生じる物理量変化を高い精度で与える。さらに、摂動後の非平衡状態における物理量変化は時間に依存し、通常用いられる時間平均による物理量算出は不可能であるため、多数組のPMD、UMDを実行しアンサンブル平均をとることで、時間依存の物理量変化を得る。
摂動
注目する力学的相互作用に比べて、相対的に小さい相互作用のこと。例えば、月と地球の運動に対して、他の天体が及ぼす影響は摂動の一種である。周期運動といった力学的に安定な挙動を示す系に摂動が加わることで、そこからの乱れを生じる。
線形応答理論
平衡状態にある系に摂動(擾乱)を加えると、系は平衡状態に戻ろうとする。その、平衡状態に戻ろうとする速さが摂動の大きさに比例する範囲で、系の特性を調べる方法論を線形応答理論と呼ぶ。
Green-Kubo公式
線形応答理論において、摂動と流速の比を輸送係数と呼ぶ。例えば、オームの法則において、抵抗値(電圧と電流の比)は輸送係数の代表である。輸送係数を微視的な観測量から計算する方法論がGreen-Kubo公式である。
アボガドロ数
質量数12の炭素原子(12C)12g中に含まれている原子の数は、6.02×1023個で、これをアボガドロ数という。原子や分子やイオンの量はアボガドロ数個の集団を単位とすると便利なので、6.02×1023個の粒子の集合を1 molと言う。1 molあたりの粒子の数をアボガドロ定数とよび、6.02×1023 mol-1である。
アンサンブル
統計力学の確率論的な考え方を明確にするために、対象系と同じ組成かつ同じ相互作用をしている系を多数個仮想的に考えて統計的集団を構成する。その仮想的な統計的集団のことをアンサンブルという。粒子数とエネルギーが指定されているミクロカノニカルアンサンブル、粒子数は一定だが外界とエネルギーをやり取りすることのできるカノニカルアンサンブルなどがある。
エルゴード仮説
力学系について、或る物理量の時間平均が位相平均(統計力学においては、特に集団(アンサンブル平均))と等しいとする仮説。平衡統計力学の基礎である等重率の原理に関する仮定であり、特別な系についてのみ厳密に証明されている。
Fokker-Planck方程式
ブラウン運動する粒子に関する分布関数 f(x, t) に関する運動方程式の一つであり、分布関数 f(x, t) に関する2階の偏微分方程式
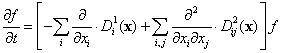
Langevin方程式
或るポテンシャル中のブラウン運動を記述する確率微分方程式。簡単なLangevin方程式は、質量 m のブラウン粒子の加速度 a が、ポテンシャルによる力 F(x) と、その速度に比例する粘性力 -βv と、ノイズ項 ηの和として表現される。
確率過程
確率変数を用いて記述することができる(時間に依存する)過程のこと。水中の花粉などのようなブラウン粒子のランダムな運動を数学的に記述するために理想化して導入された。近年、為替変動など、ランダムな振る舞いを性質として持つようなシステムへも応用されている。
確率的運動方程式
確率過程に対する確率微分方程式のこと。Langevin方程式やFokker-Planck方程式が代表的なものである。前者は、ランダム力が働いている質点としてモデル化できる現実系に適用され、後者は、そのようなランダム力に関して平均化して、質点の運動状態を確率分布としてまとめて微分方程式として表現したものである。
緩和過程
非平衡状態が平衡状態に戻る過程(変化の道筋)。分子の電子状態や分子構造、分子間ネットワーク構造などが、あるエネルギーの高い状態から低い状態へ遷移していく過程のことを指す。緩和過程を特徴付ける量として緩和時間(時定数)が挙げられる。理想的な系ではエネルギーは時間について指数的な減衰を示す。
振動励起
分子内原子群の振動運動がエネルギー的に高い運動状態に移り変わること。通常、振動運動が量子化されている場合を念頭にして、離散化された振動エネルギー状態(振動準位と呼ぶ)が、より高い振動エネルギー状態に移ることを振動励起という場合が多い。
粗視化
原子個々の位置や速度からなる詳細な物理量の情報を適当なスケールで平均して特徴的な少数の物理量で表現すること。疎視化とも。そのスケールで特徴付けられる性質を理解するため、あるいは、着目している物理量に対して寄与の小さい物理量の自由度を減らすために行われる。例えば、ブラウン運動を表すLangevin方程式では、溶媒分子が及ぼす力を摩擦力とランダム力の二つに粗視化している。
等重率の原理
温度や圧力などの熱力学的な変数で指定される状態を巨視的状態と言うのに対して、個々の原子 i の位置 q i や運動量 p i などの力学的な変数で指定される状態を微視的状態と言う。熱平衡状態にある孤立系においては、どの微視的状態も等しい確率で実現されるというのが等重率の原理である。ミクロカノニカル集団(あるいはアンサンブル)は、{q i, p i} からなる相空間において、当エネルギー面上の微視的状態が等確率で実現されることから、定義される。ミクロカノニカル集団は、孤立系が十分放置されて熱平衡に達した場合を表現している。
統計平均
或る統計的集団におけるデータセットについての平均。統計力学においては集団(あるいはアンサンブル)平均を意味することが多く、時間変化するデータセットについての平均である時間平均とは区別して用いられる。本来は可能な全ての状態に関する集団平均でなければならないが、実用上、与えられたデータセットに関する平均値を推定値として用いる。
非定常状態
定常状態ではない状態。平衡定常状態でないどころか非平衡定常でもない状態。定常、平衡という言葉を特に区別することなく用いていることもあり、単に非平衡状態を指すこともある。定常状態に到達するまでに通過する状態。
熱浴
取り扱う対象としての物理的な体系を単に系と呼ぶ。その系に対して熱的に相互作用する十分大きな系のことを熱浴という。例えば、溶質分子に対して溶媒全体のことを熱浴と呼ぶことがある。また、分子動力学シミュレーションにおいては、系の温度や圧力を制御するための仮想粒子のことを指すことがある。
定常状態
時間変化のない平衡状態とは異なり、時間の原点をずらしても変化しない状態。例えば、流速が一定の系の状態。定常な確率過程 x(t) について、その相関関数 R(t1, t2) = < x(t1) x(t2) >は、τ = t1 - t2 の関数となり、R(t1, t2) = R(τ) = R(-τ) を満たす。
非定常状態
定常状態ではない状態。平衡定常状態でないどころか非平衡定常でもない状態。定常、平衡という言葉を特に区別することなく用いていることもあり、単に非平衡状態を指すこともある。定常状態に到達するまでに通過する状態。
平衡状態
熱力学特性関数が最大または最小となる状態、特にエントロピーが最大となる状態。この状態では巨視的な量が時間的に変化しないことから、これを平衡状態の定義とすることもある。孤立系を十分放置しておくと、最終的には平衡状態が実現される。
非平衡状態
平衡状態ではない状態。つまり、エントロピーが最大になっていない状態。この状態にある孤立系を長時間放置することにより、最終的には平衡状態が実現される。
分子動力学シミュレーション
2体またはそれ以上の(質点と近似された)原子間にポテンシャルを仮定し、ニュートンの運動方程式を数値的に解くことにより、系全体の運動を解析する方法。電子や核の量子効果を取り入れた手法もある。AMBER、CHARMM、NAMD、GROMACSなどの汎用ソフトウェアがある。