孤立反応から凝集系化学反応へ
今日、気相孤立反応では反応物の幾何構造やポテンシャルエネルギー面といった情報が比較的容易に得られる。一方、液相中といった凝縮系化学反応では、反応物である溶質分子群はもちろん、その周囲の膨大な数の溶媒分子が関与するため、非常に難しい。我々は、凝集系化学反応における溶質分子の溶媒和構造やそのダイナミクスを明らかにする理論的手法の1つとして自由エネルギー勾配法(Free Energy Gradient method; FEG method)を提唱し、様々な凝集系化学反応に対して適用した。
水溶液中グリシンの異性化反応に関する理論的研究
グリシンは最小のアミノ酸である。気相中では非イオン性分子であり、双性イオンは安定には存在できない。一方で、水溶液中で中性型と双性イオン型とが共存していることが知られている。我々は、自由エネルギー勾配法を用いて、グリシンの異性化反応の定量的な再現とその安定状態及び遷移状態の完全最適化を行った。図1に、自由エネルギー勾配法により明らかになった水溶液中グリシンの異性化反応の自由エネルギープロファイル(横軸は極限的反応座標)を示す。単独では中性型で安定に存在するグリシン分子(左吹出し図)は、水溶液中では双性イオン型(右吹出し図)で安定に存在し、中性型との間には明確な遷移状態(中央吹出し図)が現れた。
また、中性型配座異性体は8つあり、それらのあいだの相対的安定性を網羅的に調査した。その結果、水溶液中では溶質−溶媒間相互作用による安定化によって溶質分子自身の不安定化が相殺されることにより、配座異性体間の自由エネルギー差は小さくなる自由エネルギー平坦化現象が見られた。
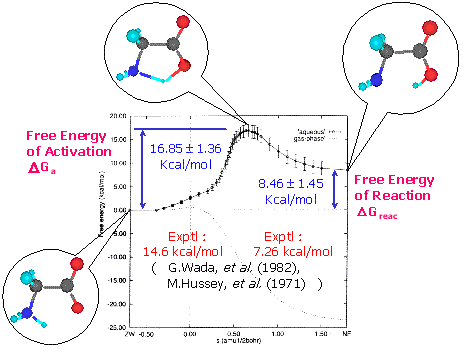
図1 水溶液中グリシンの異性化反応の自由エネルギープロファイル
【参考文献】
- N. Okuyama-Yoshida, K. Kataoka, M. Nagaoka, T. Yamabe, J. Chem. Phys., 113, 3519 (2000).
- N.Takenaka, Y.Kitamura, Y.Koyano, T.Asada, M.Nagaoka, Theor. Chem. Acc., 130(2-3), 215 (2011).
- Y.Kitamura, N.Takenaka, Y.Koyano, M.Nagaoka, Chem. Phys. Lett., 514(4-6), 261 (2011).
水溶液中でのメンシュトキン反応およびアンモニアイオン化反応に関する理論的研究
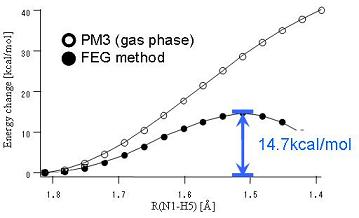
我々は、非対称反応系であるメンシュトキン反応(H3N + CH3Cl → H3NCH+ + Cl-)とアンモニアイオン化反応(H3N + H2O → H4N+ + OH-)の遷移状態決定のためにFEG法を適用した。これらの反応は、アンモニアと求核剤(ここでは、CH3ClとH2Oのこと)を含んでいる。アンモニアは加圧により容易に液化し、水への溶解度が非常に大きいという特異な性質を多く持った物質である。
我々は、水溶液中のアンモニアイオン化反応についても同様に、構造最適化を行い、自由エネルギープロファイルを求めた。図2のように、気相中(白丸)ではアンモニア分子に水分子のプロトンが近づくにつれて急激に不安定化し、遷移状態が観測されないが、水溶液中(黒丸)では明確な遷移状態が観測されることが判った。このイオン化反応の活性化自由エネルギーの計算値(14.7kcal/mol)は、実験値(9.57kcal/mol)をやや上回った。
【参考文献】
- H. Hirao, Y. Nagae, M. Nagaoka, Chem. Phys. Lett., 348, 350 (2001).
- Y. Nagae, Y. Oishi, N. Naruse, M. Nagaoka, J. Chem. Phys., 119, 7972 (2003).
- M. Nagaoka, Y. Nagae, Y. Koyano, Y. Oishi, J. Phys. Chem. A, 110(13), 4555 (2006).
- Y. Koyano, N. Takenaka, Y. Nakagawa, M. Nagaoka, Bull. Chem. Soc. Japan, 83(5), 486 (2010).
パラニトロフェノールの紫外可視吸収スペクトルの理論的研究
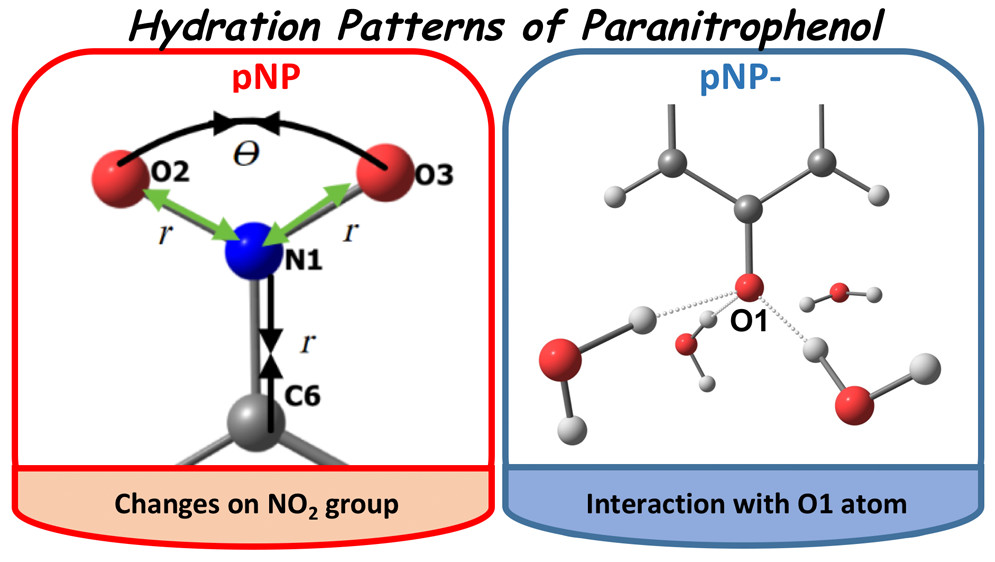
図3 水溶液中のパラニトロフェノールの水和配置
また近年、我々は、ソルバトクロミズムシフトを示す水溶液中パラフェノールの紫外可視(UV-vis)吸収スペクトルを調査した。その原子論的起源を明らかにするために、多配置電子状態方法論のひとつであるCASPT2法とFEG法を組み合わせた。その結果、実験値と近い計算値が得られた。PCMの結果と比較することで、ソルバトクロミズムシフトは主にあらわな溶媒モデルによって記述される溶媒効果による溶質の構造変化と溶媒和形成に起因することが明らかになった。
【参考文献】
- C. Bistafa, Y. Kitamura, M. Nagaoka, S. Canuto, J. Phys. Chem. B, 122(8), 9202 (2018).
振動スペクトルを解析するための理論的方法論の開発
化学反応を理解するうえで、分子系の構造情報(安定構造、中間体およびそれらを結ぶ遷移構造)に加えて、対象系の運動情報(赤外・ラマンスペクトル)がたいへん役に立つ。基準振動数解析(Vibrational Frequency Analysis; VFA)は、振動スペクトルとの比較のみならず、平衡定数や反応速度といった化学反応の起こり易さも議論可能な解析手法としてGAUSSIANなどの量子化学計算パッケージにおいても標準的に実装されている。しかし、凝集系の溶質分子の運動は、周辺環境中の溶媒分子との相互作用によって、孤立系での運動に比べて複雑になる。
我々は、凝集系での分子振動を効率的に求める近似的方法論として双振動解析手法(Dual approach to vibrational spectra)を提案し、振動スペクトルに対する水素結合などの微視的な溶媒効果の影響を調査している。図4に、液体中の水分子のIRスペクトルを示した。
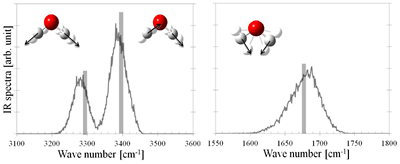
図4 液体中水分子のIRスペクトル
【参考文献】
- H. C. Georg, T. S. Fernandes, S. Canuto, N. Takenaka, Y. Kitamura, M. Nagaoka, In Practical Aspects of Computational Chemistry III; J. Leszczynski, M. K. Shukla, Eds.; Springer; New York, USA, 2014.
- Y. Kitamura, N. Takenaka, Y. Koyano, M. Nagaoka, J. Chem. Theor. Comp., 10(8) 3369 (2014).
- Y. Kitamura, N. Takenaka, Y. Koyano, M. Nagaoka, In Quantum Modeling of Complex Molecular Systems; J-L. Rivail, M. Ruiz-Lopez, X. Assfeld, Eds.; Springer; New York, USA, 2015.
高効率・高精度自由エネルギー勾配法の理論的方法論の開発
自由エネルギー勾配(Free Energy Gradient, FEG)法は、溶媒中溶質の自由エネルギー面を探索するための優れたツールである。しかしながら、多くの場合において、第一原理量子化学(ab initio QM)計算は、大きなシステムサイズでは高負荷であるので、計算負荷を高精度FEG法の効率的方法論の開発が提案されている。従来法へQM法によって記述される溶媒分子の分極効果を再現する応答カーネル近似を導入することによって、従来のFEG法に比べて、計算時間を著しく減少させることが可能であることを示した。また、自由エネルギー微分量を正確に得るための混合型自由エネルギー理論(FEP-FEG法)を提案し、水溶性水分子の実験的物理量を低コストで再現できることを示した。
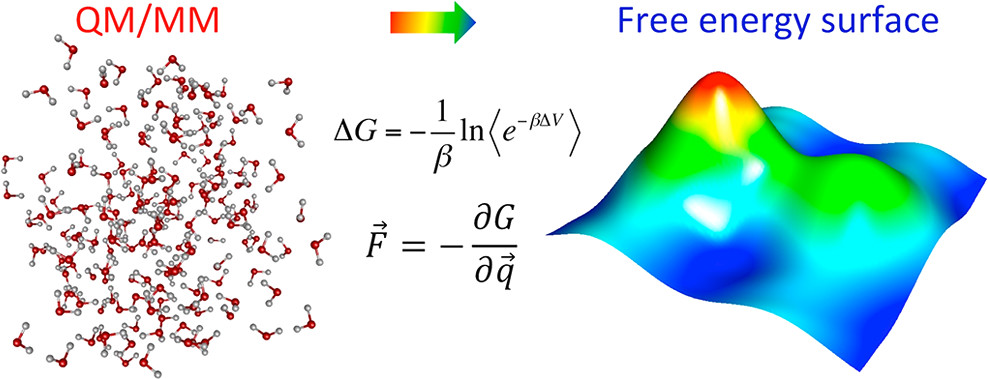
図5 FEP-FEG法の概念図
【参考文献】
- T. Asada, K. Ando, K. Sakurai, S. Koseki, M. Nagaoka, Phys. Chem. Chem. Phys., 17(40), 26955 (2015).
- N. Takenaka, Y. Kitamura, M. Nagaoka, J. Phys. Chem. B, 120(8), 2001 (2016).
- C. Bistafa, Y. Kitamura, M. T. C. Martins-Costa, M. Nagaoka, M. F. Ruiz-Lopez, J. Chem. Theory Comput., 14(6), 3262 (2018) (A selected article as cover image of the JCTC June 2018.).
メチルリチウムの会合状態に関する理論的研究
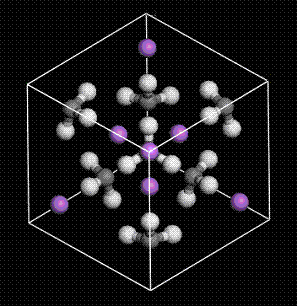
有機金属反応剤アルキルリチウムは強塩基であるため、求核試薬として有機合成上、非常に重要な役割を果たしている化合物である。その一種であるメチルリチウムCH3Liの結晶構造は、実験より四量体の体心立方格子(各メチル基はリチウム原子に対してスタッガード配座を呈する(図6))として存在することが知られている。
また、気相中での孤立系メチルリチウム(その四量体は結晶構造のそれとは異なり、各メチル基がエクリプス配座をとる(図7))の構造についても、実験や理論的手法による解釈が成されている。
一方、有機溶媒中におけるメチルリチウムは、THF中で四量体、エーテル中では四量体と二量体間の化学平衡状態で存在することが実験的に知られているものの、特定されておらず、その会合状態に関する詳細な研究は未だ成されていない。
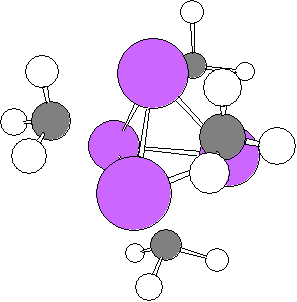
本研究では、これまで実験的に観測されている結晶中および気相中におけるメチルリチウムのメチル基配座特性の起源を分子軌道計算等の計算化学的手法を用いて明らかにし、その結果を踏まえて有機溶媒中における会合状態を分子動力学シミュレーションを用いた自由エネルギー勾配法から特定し、メチルリチウムに関する気相中、結晶中および溶液中での構造情報(配向性や会合体)に関する系統的理解と、実験、理論との相互理解を目指す。
【参考文献】
- Y. Ohta, A. Demura, T. Okamoto, H. Hitomi, M. Nagaoka, J. Phys. Chem. B, 110(25), 12640 (2006).
グリシン
グリシンとはアミノ酢酸のことである。分子式はNH2CH2COOHである。タンパク質を構成するアミノ酸の中で最も単純な形を有する。不斉炭素を持たないために、生体を構成するアミノ酸としては唯一 D-, L- の立体異性が存在しない。
中性分子
分子がプラスにもマイナスにも帯電していない中間の状態のことである。例えば、水分子や酸素分子、アンモニア分子などが挙げられる。ここでいう中性とは酸性、塩基性に対する中性のことではない。
イオン
電荷をもつ原子または原子の集団のことである。正、負の電荷をもつものをそれぞれ陽イオン(カチオン)、陰イオン(アニオン)といい、電解質溶液中などには電気的に等量の陽イオンと陰イオンが含まれている。気相や固相中にもイオンは存在する。
安定状態
等温かつ定圧の条件下において、運動形式間で分子が変化しうる構造において、最も自由エネルギーの低い状態のことである。分子がとりうる構造の自由エネルギー面を山と谷で表すとすると、谷底の部分のことを指す。
遷移状態
化学反応の過程で原系から生成系に変換するときに通る最も自由エネルギーの高い状態のことである。例えば、2つの分子の衝突によって反応が開始するとき、力学的エネルギーが分子内部のエネルギーに変換され、元の構造からゆがんだ構造をとるが、その中で最も自由エネルギーの高い状態のことを指す。
アンモニア
アンモニアは分子式 NH3 で表される無機化合物である。常温常圧では無色で刺激臭のある気体であり、加圧により容易に液化し、水への溶解度が非常に高いといった特異な性質を持つ分子である。化学工業では最も基礎的な窒素源としてきわめて重要である。
自由エネルギー
熱力学における状態量の1つ。温度・体積一定の過程における自由エネルギーをヘルムホルツの自由エネルギーF(またはA)、温度・圧力一定の過程における自由エネルギーをギブズの自由エネルギーGと呼ぶ。
自由エネルギー勾配法
溶液中での溶質分子の構造最適化手法の一つ。自由エネルギー面上における溶質分子が受ける力、すなわち負の勾配から、溶質構造を更新する。同様の操作を繰り返し行い、ゼロ勾配となったときの構造を最適化構造とする。反応座標に沿って溶質分子の構造最適化を実行することで、自由エネルギー面上の極値である反応系と生成系とを結ぶ自由エネルギープロファイルを求めることが出来る。
基準振動数解析
基準振動数解析とは、分子振動が調和的にふるまうと仮定して、振動運動を基準振動の重ね合わせとしてあらわす解析法のこと。平衡構造でのエネルギーの二次微分(ヘシアン)を要素とするヘシアン行列を対角化することで基準振動数およびその振動モードを求めることができる。
平衡定数
化学反応が平衡状態に達した時の物質の存在比のこと。これは、分子の熱力学量から求められ、分子の内部エネルギーに加えて分子の並進・回転および分子内振動の寄与を考慮することが必要である。基準振動数解析から得られた振動数により、次式のように平均振動励起エネルギー および振動エントロピー を評価できる。
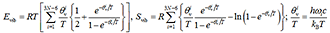
自由エネルギーを反応物および生成物で評価することで、化学反応の平衡定数を求めることができる。
反応速度
化学反応の反応物あるいは生成物に関する各成分量の時間変化率を表す物理量。通常、反応速度を表現する式は濃度のべき関数として表現される。絶対反応速度論に基づくと、遷移状態X‡での基準振動から反応速度定数を求めることもできる。遷移状態を反応座標に沿った1つの振動モードについて運動しているとみなすと、反応系と遷移状態間との平衡条件から、反応速度は以下のように与えられる。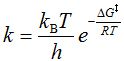
メチルリチウム (CH3Li)
C-Li結合を持った化合物である有機金属反応剤アルキルリチウムRLi (R:アルキル基)の一種。主にハロゲン化アルキルと金属リチウムとの反応により合成される。また溶液中で会合体を形成し、配位性化合物の添加で会合度が低下するので反応性に大きく影響する。CH3LiはRLiの内、最も簡単な化合物で、主に化合物のメチル化に用いられる。
求核試薬
電子密度の低い原子(主に炭素)へ反応し、多くの場合、結合を作る化学種のこと。Grinard(グリニャール)試薬や有機リチウム化合物を代表とする各種有機金属試薬は、多様な基質に対して高い反応性を示すことから、有機合成上、C-C結合を得たい時に用いられる非常に重要な求核試薬である。
体心立方格子
結晶構造の一種。立方体形の単位格子の各頂点と中心に原子が位置する。略称BCC(Body-Centered Cubic)格子。充填率68%(最充填ではない)、近接する原子の数(配位数)8個、単位格子中の原子の数:2個。アルカリ金属にこの構造を持つものが多い。
スタッガード配座とエクリプス配座
例えば、X-A-B-Y結合の内、A-B周りの立体配座を考える。これは結合X-Aと結合B-Yの二面角で区別できる。二面角が60度、180度の場合、A上とB上の置換基が互い違いになり、これをスタッガード(ねじれ型)配座という。一方、二面角が0度、120度の場合、これらは互いに重なり、これをエクリプス(重なり型)配座という。
分子軌道計算
原子軌道に対応して、分子全体に広がる一電子空間軌道関数である分子軌道によって、分子を構成する個々の電子の状態が記述されると考える。この分子軌道を計算して、分子の電子状態を求める方法が分子軌道法である。
分子動力学シミュレーション
2体またはそれ以上の(質点と近似された)原子間にポテンシャルを仮定し、ニュートンの運動方程式を数値的に解くことにより、系全体の運動を解析する方法。電子や核の量子効果を取り入れた手法もある。AMBER、CHARMm、NAMD、GROMACSなどの汎用ソフトウェアがある。