| │サイトマップ│Japanese│English│ |
-
進学希望者の方へ
-
研究内容
- 物質の変化を計算科学する
- 非平衡系
- 凝集系化学反応
- マクロ化学現象
- 生命現象
- マルチスケール情報処理
- 産業応用
- 2023年度
- 2022年度
- 2021年度
- 2020年度
- 2019年度
- 2018年度
- 2017年度
- 2016年度
- 2015年度
- 2014年度
- 2013年度
- 2012年度
- 2011年度
- 2010年度
- 2009年度
- 2008年度
- 2007年度
- 2006年度
- 2005年度
- 2004年度
- 2003年度まで
- 2000年度まで
- 2019年度
- 2018年度
- 2017年度
- 2016年度
- 2015年度
- 2014年度
- 2013年度
- 2012年度
- 2011年度
- 2010年度
- 2009年度
- 2008年度
- 2007年度
- 2004〜2006年度
- 2003年度
コンセプト研究内容学会・セミナー
オープンセミナー
参考文献
設備
-
メンバー
- スタッフ
- 研究生・学生
- OB・OG
- OB・OGの声
- 2018年度〜
- 2015〜2017年度
- 1999〜2014年度
メンバーアルバム -
アクセス
- アクセスマップ
- 東山キャンパスマップ
- 風景(外観)
- 書類宛先
- 受験案内 ※リンク
アクセス住所 -
関連サイト
並行コンピューティングからマルチスケール情報処理へ
今日、実験技術の精緻化に伴って、簡単なモデルでは、もはや解釈や結論を出し得ない構造データや物性予測が次々と提出されている。こうした状況を考えると、原子階層での化学反応シミュレーションとそれと調和した統計理論の必要性は万人の認めるところである。実際、近年の実験・理論両面からの革新的成果から、短時間スケールや微小空間領域において自然がもつ、巨視的世界から見ると“非常識”な不思議な振る舞いが次々と明らかにされている。こうしたスケールでは明らかに原子が主役であり、その集団ダイナミクスの“妙”を理解することが急務となっている。つまりニュートン方程式を単に解くだけでは理解できず、ボルツマン方程式や流体力学方程式を直接当て嵌めるのにも無理があるような時空スケール現象が問題となってきている。
我々は、シミュレーション技法としての並行コンピューティング技術を駆使し、凝集化学反応系に対して適用可能なQM/MM‐MDシミュレーション実行環境を整備したいと考えている。さらに、大規模原子情報の疎視化理論と再構成技法を構築してマルチスケール情報処理を実現し、新物質・新材料の開発指針確立のための実用的基盤と知的資産の形成に貢献する。
QM/MM‐MDシミュレーションIFの開発の並行コンピューティングの実現
凝集化学反応系の非経験的(ab initio)分子動力学(MD)シミュレーションを可能とするために、ab initio分子軌道(MO)法とMD法とを連携させるためのインターフェイス(IF)、QM/MM-IFを開発する。また、或る熱力学的状態に対応する一つの初期位相分布から選ばれた多数の初期条件群のMD計算を、複数のCPU(あるいはノード)で並行して実行させるアンサンブルMD(EMD)法を開発する(図1)。さらにその計算結果を高速ネットワーク(あるいは高速バス)によって集約し、統計情報の時間空間変化をリアルタイムで追跡することを可能にする並行コンピューティングを実現する(図2)。
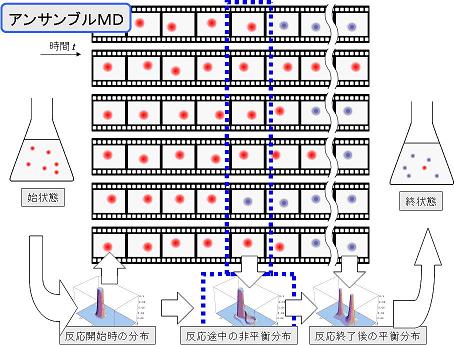
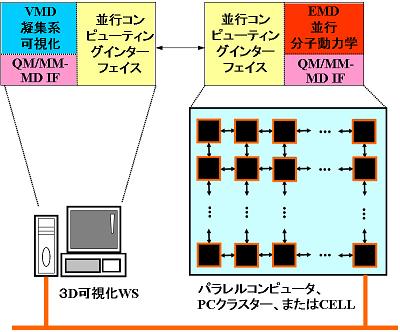
図2 並行コンピューティングの概念図。EMD構成要素の非同期通信過程への分割と統合。
AMBER-PAICSインターフェイスの開発 −高分子系の電子状態計算への展開−
高分子系や生体分子系等の大規模な凝集化学反応系への適応を目的として、QM/MM-MD法のQM計算にフラグメント分子軌道(FMO)法を適用したFMO-QM/MM-MD法を開発した。FMO法とは、QM領域内を幾つかのフラグメントに分割することにより、QM計算の計算時間やコストを大きく削減することが可能となるab initio MO法の一つである。生体高分子系のMDシミュレーション実行プログラムとして、よく知られたAMBERと、FMO法計算用プログラムの一つであるPAICS(共同研究者である石川岳志氏が開発)とを組み合わせ、AMBER-PAICSインターフェイス(AP-IF)を構築した(図3)。
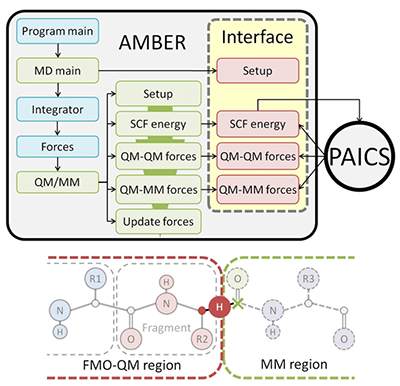
図3 AMBER-PAICSインターフェイスのフローチャート(上)とFMO-QM/MM-MD法での領域分割例(下)
凝集化学反応系のマルチスケールシミュレーション技法の開発
一般的に、化学反応を研究するためには電子状態の解析が不可欠であるが、その計算コストは非常に高い。したがって、化学反応に直接関与する溶質とその周辺の溶媒だけをQM領域として量子力学(QM)的に取り扱い、その他の溶媒はMM領域として分子力学(MM)的に扱うことができれば、計算精度と計算コストのバランスを考えると最も望ましいと考えられている。ただし、この場合には、QMとMMという異なる特性スケールの領域を扱うことから生まれる不連続性の問題が生じる。
我々は、QM領域とMM領域の間に遷移(T)領域を設けて、多段階のQM/MM計算を行うことにより、2つの領域間をスムースに繋げることができる分子数適用階層型(Number-Adaptive Multiscale) QM/MM-MD法を開発した(図4)。現在、並行コンピューティング技術との連携をさらに進めて、凝集化学反応系シミュレーションの実用的なサンプリング手法の確立を目指している。
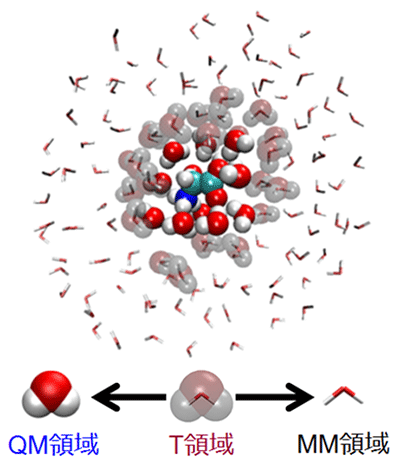
図4 分子数適応階層型QM/MM-MD法の概念図。図中では、溶質グリシン分子とその周辺の溶媒水分子をQM領域として取り扱った。
N.Takenaka, Y.Kitamura, Y.Koyano, M.Nagaoka, Chem. Phys. Lett., 524, 56 (2012). N.Takenaka, Y.Kitamura, Y.Koyano, M.Nagaoka, J. Chem. Phys., 137, 024501 (2012).
疎視化理論と再構成技法によるマルチスケール情報処理の実現
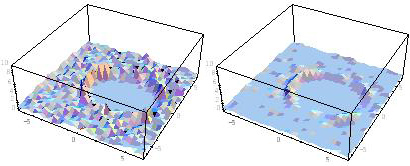
QM/MM-MDシミュレーションを具体例に適用して大規模原子運動情報(個別原子の位置・運動量の時系列データ)を求め、微小時空間の疎視化窓における有限長時空間データから得た時空数密度分布を得る。これを入力初期分布とする体系的時空分布再構成技法を開発する。実行例として、図5に水溶液中HF分子の振動緩和過程に対して本手法を適用して得た水溶媒系の密度分布を示した。図5(左)と図5(右)には、それぞれ初期分布と最適分布の三次元表現を示したが、最適分布図5(右)の解像度に相当する初期分布を、MDシミュレーションの元データのみから得ようとすると、図5(左)を描くために必要とした初期データの数十倍が必要である。この再構成技法は、時間空間分布解析の計算コストを実効的に低減できるため、将来、ペタ級実演算性能を利用した凝集反応系マルチスケールシミュレーション実現の際には、さらに数桁上の実効性能を得る基盤技術として供する可能性がある。
QM/MM
反応に関与する領域を量子力学(QM)的に取扱い、それ以外の領域を古典力学的(MM)的に取り扱う方法。このような取扱いにより、大きな系に対しても、計算精度を保ちながら、計算コストを大幅に削減することが可能である。
アンサンブルMD(EMD)法
同一の熱力学条件下(温度、圧力など)において、相関のない多数の初期配置を用いて多並行の分子動力学(MD)計算を行い、アンサンブル平均(もしくは時間平均との組み合わせ)により熱力学量を算出する方法。また、熱力学量の統計誤差の評価を行う場合にも用いられる。
フラグメント分子軌道(FMO)法
巨大分子系を適切なサイズのフラグメントに分割し、周囲のフラグメントからの静電ポテンシャルを考慮してフラグメント(モノマー)とフラグメントペア(ダイマー)などの電子状態を計算する。次に、これらのエネルギーやエネルギー勾配を用いて、系全体に対応する値を再構成する。この方法は北浦らにより開発された。
FMO-QM/MM-MD法
反応部位のみをQM的、その周囲を分子力学(MM)的に取り扱うQM/MM-MD法において、そのQM計算にフラグメント分子軌道(FMO)法を適用したMD法。