素反応から複合化学反応へ
一般に化学現象とは幾つかの素反応過程が(ミクロに見ると)あちらこちらで連続して起こった結果として生じる。個々の素反応に注目すると、相空間における或る領域間の遷移として表せるが、反応系が多くの時間を安定領域で費やすため、一回の素反応そのものは(一度起こり始めればいかに早く短時間スケール(〜ps(ピコ秒))で起こったとしても)極めて稀にしか起こらない希少現象(レアイベント(Rare event))である。ところが、分子群の立体特異性や集合体構造は、長時間スケール(≧μs(マイクロ秒))での複合的な化学反応(群)の積み重ねの結果によって生じる超希少現象として生まれるため、従来の計算科学的な方法ではシミュレートすることが全く不可能である。そこで、当研究室では大規模な複合化学反応系(Complex chemical reacting systems)に対する実用的なアトミスティックシミュレーションの実現を目指して、その基盤技術となりうるレッドムーン法(混合モンテカルロ(MC)/分子動力学(MD)反応法)を提案し開発している。
レッドムーン法(混合MC/MD反応法)
レッドムーン法(混合MC/MD反応法)とは、短時間スケールで起こる分子運動(分子の並進、回転および振動)には古典的な分子動力学(MD)計算を使い、長時間スケールで起こる化学反応などには確率的なモンテカルロ(MC)法によって取り扱う方法論である。つまり、対象系の動的な状態変化を考慮しながら多種類の化学反応などを多数回実現させて、従来では実現できなかった数百Å×μs〜msの時間・空間スケールの化学現象を取り扱うことができる方法なのである。このような化学反応などの希少現象を促進する機構(Rare event-driving mechanism)によって、最終的に全系の化学平衡状態(あるいは定常状態)が生成される。
レッドムーン法の概念図を図1に示す。
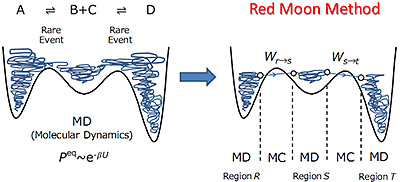
図1 レッドムーン法(混合MC/MD反応法)の概念図
相空間中の領域RでMD計算を行い、反応の条件を満たす分子内/間の原子対の候補を探索する。次に、選択された反応候補に対して、仮想的に分子を反応させ、領域Sへと移行させる。この際、反応前後のポテンシャルエネルギー差ΔUrs (= Us - Ur)を用いて、遷移確率
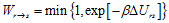
に従い、メトロポリス法により遷移の可否を判定する。こうしたMC法とMD法からなる一連のサイクル(MC/MDサイクル)を繰り返すことにより、反応による状態変化を促進し、大規模な複合化学反応系に対する長時間スケールのシミュレーションを実現する。
我々は、この種の混合MC/MD法の一群を、Rare event-driving methodology of necessityのアクロニム(頭字語)から、レッドムーン法(Red Moon method)と呼んでいる。その命名への想いは以下の文献を参照してほしい。
【参考文献】
- M. Nagaoka, Y. Suzuki, T. Okamoto, N. Takenaka, Chem. Phys. Lett., 583, 80-86 (2013).
- Y. Suzuki, M. Nagaoka, J. Chem. Phys., 146, 204102 (2017).
2-クロロブタンのラセミ化反応
立体化学の分野において、2-クロロブタンは、不斉炭素を有する典型的な有機化合物の一つとして知られ、その立体構造が異なる二つの立体異性体(光学異性体R体及びS体)が存在する。有機溶媒中において2-クロロブタンは塩素原子が何度も解離と結合をして異性化を繰り返すため、R体とS体が同比率となるラセミ体として存在することが知られている。
N,N-ジメチルホルムアミド(DMF)溶媒中に2-クロロブタンのR体のみを混合させた溶液系に混合MC/MD反応法を適用した。図2の動画にはMC/MDサイクル数に対する2-クロロブタンのR体とS体、及び2-ブチルカチオンとCl-イオンの混合状態の変化と分子数変化を表すグラフを示した。MC/MDサイクルが進行するにつれ、2-クロロブタンの分解・生成が繰り返し起こり、R体とS体の分子数が変化する様子が見られる。最終的に、全系は、R体とS体とが同比率(〜0% e.e. (鏡像体過剰率))で揺らぐ平衡状態に到達する。つまり混合MC/MD反応法を適用して、R体の2-クロロブタンのみが存在する始状態から始めて、R体とS体が同比率になるラセミ化反応を実現することを示せた。
【参考文献】
- M. Nagaoka, Y. Suzuki, T. Okamoto, N. Takenaka, Chem. Phys. Lett., 583, 80-86 (2013).
実時間反応シミュレーション
レッドムーン(Red Moon: RM)法におけるMC/MDサイクル(RMサイクルとも呼ぶ)の繰り返しによって、大規模な複合化反応系の長時間シミュレーションを実現可能とした。このRMサイクルを横軸にして、縦軸には反応系の何らかの物理量を示すことで、RMサイクルの進行に伴う系の状態変化を知ることができる。ここで、さらに我々は、このRMサイクルを実際の時間(実時間)として解釈する理論を構築することで、化学反応系の実時間反応シミュレーションの実現を試みた。
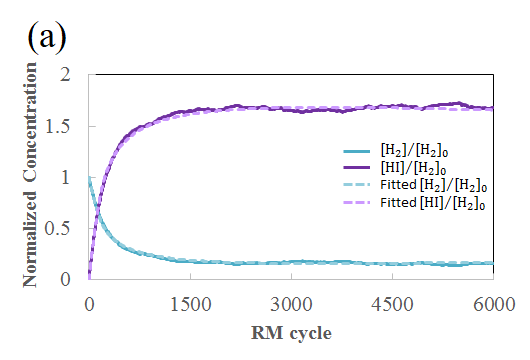
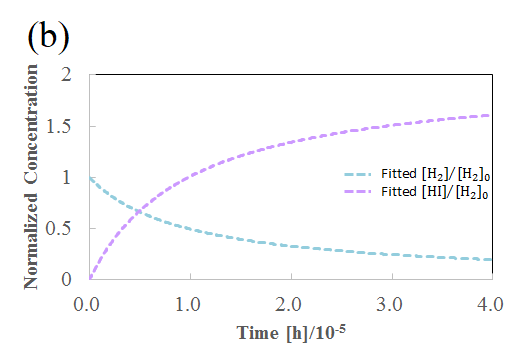
図3(a)RMサイクルと(b)時間に対するH2分子とHI分子の濃度変化
そこで先ずは、高校化学においてもよく知られる二次の可逆反応系(H2+I2⇋2HI)を対象に、RMシミュレーションを行った。その結果、図3(a)のようにRMサイクルに対するH2分子とHI分子の濃度変化が得られた。本結果から得られたあるRMサイクルkにおける各成分濃度[H2]k, [I2]k及び[HI]kと、対象系の正反応と逆反応の速度定数kfとkbを用いて、反応速度式から導いた次式によって、あるRMサイクルNまでの経過時間tが算出できる。
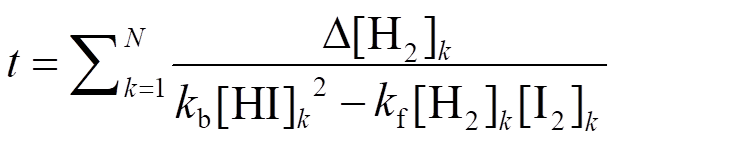
本式によって、図3(b)のように時間に対するH2分子とHI分子の濃度変化を解析することができた。 上記の式は、本対象系よりも複雑な複合化学反応系への応用が十分に可能であり、レッドムーン法によって実時間反応シミュレーションが実現可能であることを示せた。
【参考文献】
- Y. Suzuki, M. Nagaoka, J. Chem. Phys., 146, 204102 (2017).
相空間
粒子の位置と運動量を変数とする座標軸によって規定される分子の運動を記述するための抽象的な次元空間。
モンテカルロ(法)
ある与えられた集合の特性を表すパラメータの値を求めたいとき、乱数を使ってその集合から要素を選び出し(サンプリングするという)、そのサンプル集団を統計処理することによりパラメータの近似値を計算する数値的手法。
平衡状態
外界の条件が一定の時、系が最終的に到達する最も安定な状態。
定常状態
時間変化のない平衡状態とは異なり、時間の原点をずらしても変化しない状態。例えば、流速が一定の系の状態。定常な確率過程 x(t) について、その相関関数 R(t1, t2) = < x(t1) x(t2) >は、τ = t1 - t2 の関数となり、R(t1, t2) = R(τ) = R(-τ) を満たす。
メトロポリス法
乱数を使って次々と新しい状態を生成してゆく過程を繰り返し、その系列の十分後の方では各状態がボルツマン分布則に従うことを保証するアルゴリズム。
不斉炭素
4種の異なる原子または基と結合した炭素原子。
立体異性体
構造式は同じだが、立体的に重ね合わせることのできない分子。
ラセミ体
系内の二つの鏡像体が等量存在する状態のこと。
鏡像体過剰率
光学純度を表し、不斉化合物の鏡像体が混合する割合e.e.(enantiomeric excess)で表される。e.e.は鏡像体の多い方の物質量から少ない方の物質量を引き、全体の物質量で割った値で表される。
ラセミ化
純粋な光学活性分子が環境要因(熱や光、あるいは酸・アルカリなど)によって異性化反応を生じ、経時変化に伴って二つの鏡像体の等量混合物になること。