| [Site Map][Japanese][English] |
-
Student Recruitment
-
Project
- Computational Science
- Nonequilibrium Systems
- Chemical Reactions
- Macroscopic Chemical Phenomena
- Life Phenomena
- Multiscale Information Processing
- Industry Applications
- Meetings
- FY 2022
- FY 2021
- FY 2020
- FY 2019
- FY 2018
- FY 2017
- FY 2016
- FY 2015
- FY 2014
- FY 2013
- FY 2012
- FY 2011
- FY 2010
- FY 2009
- FY 2008
- FY 2007
- FY 2006
- FY 2005
- FY 2004
- FY 2003
- FY 2000
- FY 2019
- FY 2018
- FY 2017
- FY 2016
- FY 2015
- FY 2014
- FY 2013
- FY 2012
- FY 2011
- FY 2010
- FY 2009
- FY 2008
- FY 2007
- FY 2004-2006
- FY 2003
ConceptResearchesMeetings & Seminars
Open Seminars
References
Facilities
-
People
- Staff
- PostDocs & Students
- OB & OG
- OB & OG Messages
- FY 2018-
- FY 2015-2017
- FY 1999-2014
MembersSnapshots -
Access
-
Link
From Molecular Motion to Nonequilibrium System
Our goal is to elucidate the origin of non-equilibrium nature which can be seen in natural phenomena. We address this issue by employing both microscopic and macroscopic theories. Macroscopically, we analyze the time evolution of spatial distribution of particles using Fokker-Planck equation etc. On the other hand, microscopically, we analyze the time evolution of molecular motion at the atomic level using molecular dynamics (MD) simulation.
Coarse-grained formulation for condensed reaction systems
Condensed systems are treated as statistical ensembles consisting of ~1023 (Avogadro number) molecules. Because an accurate analysis of the system requires parallel computation of Newtonian equation with the ~1023 degrees of freedom, it is practically impossible to execute such a huge number of degrees of freedom system even if we can use the state-of-the-art supercomputer. Thus it is indispensable to employ coarse graining to reduce the number of degrees of freedom.
Kramers proposed stochastic equations of motion (e.g., Langevin formalism and Fokker-Planck formalism), where the dynamics is described along reaction coordinates of phenomenon. These formalisms assume that solvent dynamics is sufficiently faster than solute dynamics. In other words, this means that we can neglect the correlations between solute dynamics and the faster solvent dynamics. However, such an assumption does not hold in real systems. To improve the traditional methodology of coarse-graining, Mori et al developed formalisms to separate multiple dynamics across different time scales. The earlier Mori's study draw our attention to chemical reaction system which led us to indicate the importance of mode-coupling between reactant molecules.
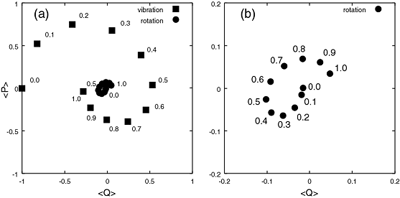
Fig.2 Induction of rotational modes by mode coupling
Statistical analysis of relaxation process by multiple MD simulations
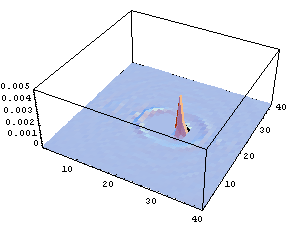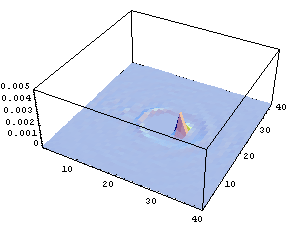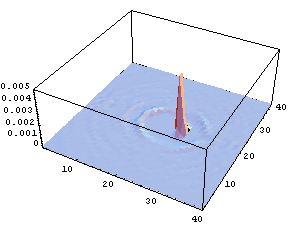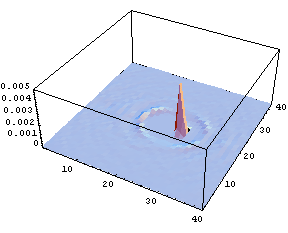
Fig.3 Spatial distribution of the number of solvent oxygen atoms
It is obvious that, since many degrees of freedom in solvent molecules around a solute molecule correlates with those in the solute molecule, chemical reactions cannot be described only by the internal degrees of freedom of solute. To simulate relaxation processes including all the degrees of freedom, MD simulation is a useful methodology. As a typical example, a hetero-nuclear solute diatomic molecule, HF, in an equilibrium aqueous solvent was vibrationally excited. By conducting excitation MD simulation for various times with ensemble averaging, the spatial distribution of the solvent oxygen atoms was obtained with high precision (Fig.3).
As a result of space-time-resolved analyses of kinetic energy and power spectra, it was revealed that energy relaxation occurs anisotropically because of the antisymmetricity of hetero-nuclear solute structure. It was also found that vibrational relaxation process of the solute molecule and structural fluctuations of solvent molecules play important roles in intermolecular vibrational couplings.
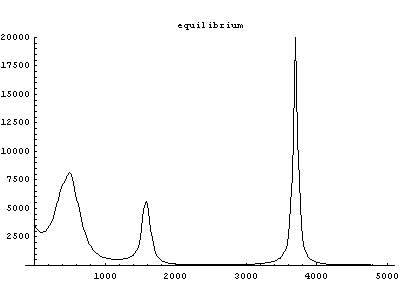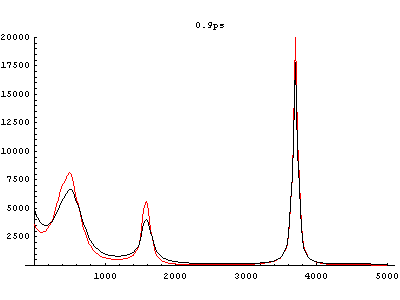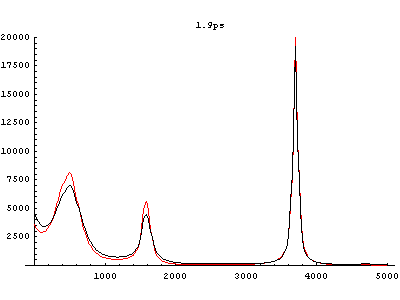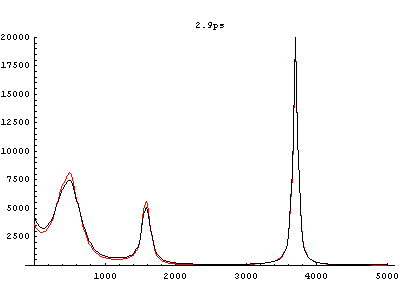
Fig.4 Power spectra of HF in aqueous solvent. (red: equilibrium state, black: vibrationally excited state)
Statistical analysis of relaxation process by perturbation ensemble MD method
As shown in the above study, it was revealed that ensemble averages over many MD trajectories of vibrationally excited systems provide us with information on the relaxation process of solute molecules. By utilizing perturbation ensemble MD (PEMD) method, in which perturbation procedure is added to the ensemble averaging, it is possible to analyze relaxation processes with higher precisions. In the PEMD method, many pairs of perturbed MD (PMD) with the perturbation and unperturbed MD (UMD) simulations without the perturbation are executed for ensemble averaging. The number of trajectory pairs should be determined to obtain target precision which is necessary to obtain experimental precision.
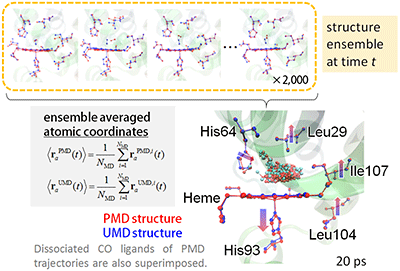
Fig.5 An example of the PEMD method to analyze a relaxation process of photolyzed carbonmonoxy myoglobin (MbCO). Structures ensemble averaged over 2,000 PMD (red) and UMD (blue) trajectories at 20 ps after the perturbation (ligand photolysis).
As an example of PEMD method, a relaxation process of photolyzed carbonmonoxy myoglobin (MbCO) was analyzed (Figure 5). Each pair of PMD and UMD was executed starting from the same initial structure with and without the perturbation (photolysis of heme-bound CO). By ensemble averaging over 2,000 pairs of PMD and UMD trajectories at 20 ps after the perturbation, the structural relaxation process after the perturbation was obtained with high precision. The result is consistent with the time-resolved X-ray crystallography. Moreover, it was also possible to analyze vibrational energy relaxation processes from the heme to the myoglobin and solvent.
M. Takayanagi, H. Okumura, M. Nagaoka, J. Phys. Chem. B, 111, 864 (2007).
M. Takayanagi, C. Iwahashi, M. Nagaoka, J. Phys. Chem. B, 114, 12340 (2010).
M. Takayanagi and M. Nagaoka, Theoret. Chem. Acc., 130, 1115 (2011).
M. Nagaoka, I. Yu, M. Takayanagi, in "Proteins: Energy, Heat and Signal Flow" (CRC Press) (Eds., D.M. Leitner, J.E. Straub)
アボガドロ定数
質量数12の炭素原子(12C)12g中に含まれている原子の数は、6.02×1023個で、これをアボガドロ数という。原子や分子やイオンの量はアボガドロ数個の集団を単位とすると便利なので、6.02×1023個の粒子の集合を1 molと言う。1 molあたりの粒子の数をアボガドロ定数とよび、6.02×1023 mol-1である。
アンサンブル
統計力学の確率論的な考え方を明確にするために、対象系と同じ組成かつ同じ相互作用をしている系を多数個仮想的に考えて統計的集団を構成する。その仮想的な統計的集団のことをアンサンブルという。粒子数とエネルギーが指定されているミクロカノニカルアンサンブル、粒子数は一定だが外界とエネルギーをやり取りすることのできるカノニカルアンサンブルなどがある。
エルゴード仮説
力学系について、或る物理量の時間平均が位相平均(統計力学においては、特に集団(アンサンブル平均)と等しいとする仮説。平衡統計力学の基礎である等重率の原理に関する仮定であり、特別な系についてのみ厳密に証明されている。
Fokker-Planck方程式
ブラウン運動する粒子に関する分布関数 f(x, t) に関する運動方程式の一つであり、分布関数 f(x, t) に関する2階の偏微分方程式
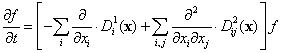
Langevin方程式
或るポテンシャル中のブラウン運動を記述する確率微分方程式。簡単なLangevin方程式は、質量 m のブラウン粒子の加速度 a が、ポテンシャルによる力 F(x) と、その速度に比例する粘性力 -βv と、ノイズ項 ηの和として表現される。
確率過程
確率変数を用いて記述することができる(時間に依存する)過程のこと。水中の花粉などのようなブラウン粒子のランダムな運動を数学的に記述するために理想化して導入された。近年、為替変動など、ランダムな振る舞いを性質として持つようなシステムへも応用されている。
確率的運動方程式
確率過程に対する確率微分方程式のこと。Langevin方程式やFokker-Planck方程式が代表的なものである。前者は、ランダム力が働いている質点としてモデル化できる現実系に適用され、後者は、そのようなランダム力に関して平均化して、質点の運動状態を確率分布としてまとめて微分方程式として表現したものである。
緩和過程
非平衡状態が平衡状態に戻る過程(変化の道筋)。分子の電子状態や分子構造、分子間ネットワーク構造などが、あるエネルギーの高い状態から低い状態へ遷移していく過程のことを指す。緩和過程を特徴付ける量として緩和時間(時定数)が挙げられる。理想的な系ではエネルギーは時間について指数的な減衰を示す
振動励起
分子内原子群の振動運動がエネルギー的に高い運動状態に移り変わること。通常、振動運動が量子化されている場合を念頭にして、離散化された振動エネルギー状態(振動準位と呼ぶ)が、より高い振動エネルギー状態に移ることを振動励起という場合が多い。
粗視化
原子個々の位置や速度からなる詳細な物理量の情報を適当なスケールで平均して特徴的な少数の物理量で表現すること。疎視化とも。そのスケールで特徴付けられる性質を理解するため、あるいは、着目している物理量に対して寄与の小さい物理量の自由度を減らすために行われる。例えば、ブラウン運動を表すLangevin方程式では、溶媒分子が及ぼす力を摩擦力とランダム力の二つに粗視化している。
等重率の原理
温度や圧力などの熱力学的な変数で指定される状態を巨視的状態と言うのに対して、個々の原子 i の位置 q i や運動量 p i などの力学的な変数で指定される状態を微視的状態と言う。熱平衡状態にある孤立系においては、どの微視的状態も等しい確率で実現されるというのが等重率の原理である。ミクロカノニカル集団(あるいはアンサンブル)は、{q i, p i} からなる相空間において、当エネルギー面上の微視的状態が等確率で実現されることから、定義される。ミクロカノニカル集団は、孤立系が十分放置されて熱平衡に達した場合を表現している。
統計平均
或る統計的集団におけるデータセットについての平均。統計力学においては集団(あるいはアンサンブル)平均を意味することが多く、時間変化するデータセットについての平均である時間平均とは区別して用いられる。本来は可能な全ての状態に関する集団平均でなければならないが、実用上、与えられたデータセットに関する平均値を推定値として用いる。
熱浴
取り扱う対象としての物理的な体系を単に系と呼ぶ。その系に対して熱的に相互作用する十分大きな系のことを熱浴という。例えば、溶質分子に対して溶媒全体のことを熱浴と呼ぶことがある。また、分子動力学シミュレーションにおいては、系の温度や圧力を制御するための仮想粒子のことを指すことがある。
定常状態
時間変化のない平衡状態とは異なり、時間の原点をずらしても変化しない状態。例えば、流速が一定の系の状態。定常な確率過程 x(t) について、その相関関数 R(t1, t2) = < x(t1) x(t2) >は、τ = t1 - t2 の関数となり、R(t1, t2) = R(τ) = R(-τ) を満たす。
非定常状態
定常状態ではない状態。平衡定常状態でないどころか非平衡定常でもない状態。定常、平衡という言葉を特に区別することなく用いていることもあり、単に非平衡状態を指すこともある。定常状態に到達するまでに通過する状態。
平衡状態
熱力学特性関数が最大または最小となる状態、特にエントロピーが最大となる状態。この状態では巨視的な量が時間的に変化しないことから、これを平衡状態の定義とすることもある。孤立系を十分放置しておくと、最終的には平衡状態が実現される。
非平衡状態
平衡状態ではない状態。つまり、エントロピーが最大になっていない状態。この状態にある孤立系を長時間放置することにより、最終的には平衡状態が実現される。
分子動力学シミュレーション
2体またはそれ以上の(質点と近似された)原子間にポテンシャルを仮定し、ニュートンの運動方程式を数値的に解くことにより、系全体の運動を解析する方法。電子や核の量子効果を取り入れた手法もある。AMBER、CHARMm、NAMD、GROMACSなどの汎用ソフトウェアがある。