From Concurrent Computing toward Multiscale Information Processing

Accompanied with the refinements of experimental techniques, structural data and the physical properties have been recently suggested which cannot be clarified or generated by using conventional simple models. Under the circumstances, the necessity of statistics theory combined with chemical reaction simulation at atomistic level is widely acknowledged. Actually, from the recent innovative results in both of theory and experiment, more and more mysterious behaviors occurring in a short-time scale and micro spatial region have been observed, and considered "absurd" from the macroscopic point of view. Obviously, characteristics of atoms must play an important part in such time and space scale and are urgently necessary to understand "strange" behaviors of their collective dynamics. In other words, the phenomena occurring in time-space scale which cannot be understood only by solving the Newton’s equation or be directly applied by the Boltzmann’s and hydrodynamic equations have become problematic.

We want to create the execution environment of QM/MM-MD simulation to be applied for condensed chemical reaction systems, using the parallel computing techniques for computer simulation. Moreover, we aim to realize the multi-scale information processing by constructing the coarse graining theory and reconfiguration technique for large atomistic information, and contribute to the formation of the practical foundation and soft asset for the establishment of guidelines to develop new substances and materials.

Development of QM/MM-MD simulation interface and realization of parallel computing

To realize ab initio molecular dynamics (MD) simulation in condensed phase chemical reaction systems, we develop the interface (IF) to combine the ab initio molecular orbital (MO) method with the MD method, i.e., QM/MM-IF. Additionally, we also develop ensemble MD (EMD) method, which enables to execute a lot of parallel MD calculations with a set of initial conditions that have been selected from various initial phase distributions corresponding to a specific thermodynamic state by using a large number of CPUs (or nodes) (see Fig.1). Moreover, we realize the parallel computing which enables to search the temporal-spatial changes of the statistical information by gathering the calculation results with the high-speed network (or high-speed bus) (see Fig. 2).

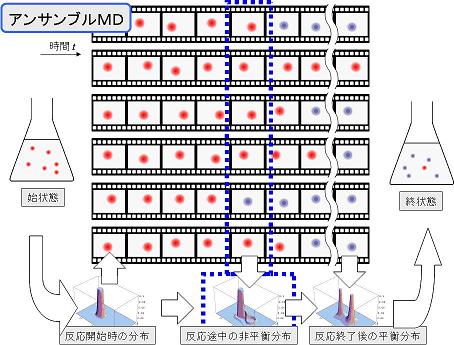
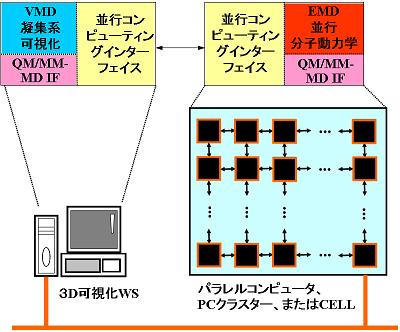
Figure 1. Schematic illustration of ensemble MD (EMD). A roll of film shows one MD trajectory with a set of initial condition by symbolized by flask.

Figure 2. Schematic illustration of parallel computing. The segmentation of the EMD building blocks into asynchronous communication processes and their integration.

[Reference] T.Okamoto, K.Yamada, Y.Koyano, T.Asada, N.Koga, M.Nagaoka, J. Comput. Chem., 32, 932 (2010).

Development of AMBER-PAICS Interface -Application to Electronic State Calculation of Macromolecule Systems-

For the purpose of applying to various reaction mechanisms in the large systems such as macromolecules and biomolecules, we developed a quantum mechanical/molecular mechanical (QM/MM) method combined with the ab initio fragment molecular orbital (FMO) method, i.e., the ab initio FMO-QM/MM method. The FMO method is one of the ab initio MO methods and offers a good compromise between chemical accuracy and computational cost by dividing the QM region into fragments. By connecting a well-known MD program AMBER with an FMO program PAICS, we have implemented an AMBER-PAICS interface (AP-IF) (Fig.3).

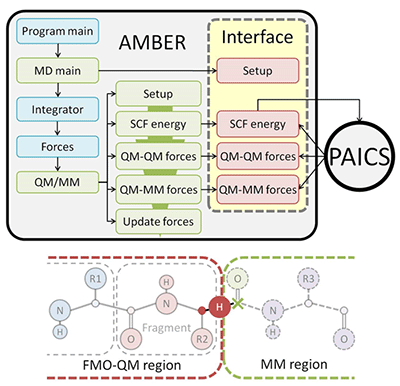
[Reference] T. Okamoto, T. Ishikawa,Y. Koyano, N. Yamamoto, K. Kuwata, M. Nagaoka, Bull. Chem. Soc. Jpn., 86, 210 (2013) (A selected paper).

Fig.3 Flowcharts of the AMBER-PAICS interface (upper) and schematic view of QM/MM fragmentation in the FMO-QM/MM method (lower)

Development of multiscale simulation techniques for aggregated chemical reaction systems

In general, to study chemical reactions, the electronic state analysis is essential, but its calculation cost is very high. Therefore, considering the balance between the calculation accuracy and calculation cost, it is reasonable to include the solute molecules and surrounding solvent molecules around them which directly participate in the chemical reactions into the quantum mechanical (QM) region and the remaining solvent molecules into the molecular mechanical (MM) one. However, there exists the discontinuity problem (about force and energy) attributed to the presence of two different characteristic scales (QM and MM regions) in solvent.

To overcome such problem, we have developed the number-adaptive multiscale QM/MM-MD method which can connect two regions smoothly by including the transition region between QM and MM regions and executing the multistep QM/MM calculations. By combining the present method with the parallel computing technology, we aim to establish the practical sampling method for condensed phase chemical reaction systems.

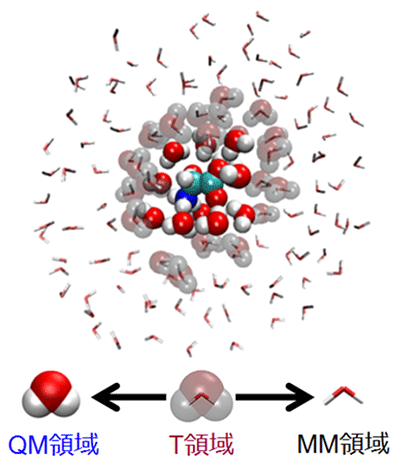
Figure 4. Schematic illustration of number-adaptive multiscale QM/MM-MD method. In this figure, a solute glycine molecule and closer solvent water molecules around it are treated as the QM region.

[Reference]

N.Takenaka, Y.Kitamura, Y.Koyano, M.Nagaoka, Chem. Phys. Lett., 524, 56 (2012).

N.Takenaka, Y.Kitamura, Y.Koyano, M.Nagaoka, J. Chem. Phys., 137, 024501 (2012).

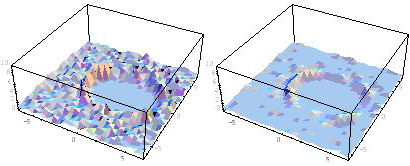
Application of multiscale information processing by coarse graining theory and reconfiguration technique

We calculate such information as the large-scale atomic motion (time-series data for position and momentum of each atom) by applying the QM/MM-MD simulations to the specific example, and then obtain the time-space number density distributions with the finite-length time-space data in the minute time-space coarse graining windows. By using them as the initial ones, we develop the systematic time-space reconfiguration technique. As an example, Figure 5 shows the density distributions of water molecules after the vibration excitation of an HF molecule in aqueous solution. Here, the left figure shows the initial distribution, while the right one shows the 3D representation of the optimized distribution by the present method. If we calculate the right figure by using only the original data of the MD simulations, the volume of required data would increase by dozens times of initial data just to draw the left figure. Therefore, this reconfiguration method can effectively reduce the calculation cost for the time-space distribution analysis. When we realize the multiscale simulations for condensed phase chemical reaction systems utilizing the peta-scale computing performance in future, such reconfiguration method will become the fundamental technology to obtain the effective performance which is several orders of magnitude larger than the original one.

Figure 5. (left) the space distribution of the atom density of the oxygen atom at lapsed time 0.3 ps after excitation (L = 13.6 A, time-space windows for analysis (dx・dt = 0.42 A × 0.42 A × 0.42 A × 0.1 ps) (lapsed time after excitation t = 0.3 ps), 32 × 32 × 32 grid points), (right) the reconfigured space distribution of the atom density of the oxygen atom by the maximum entropy method (MEM) (L = 13.6 A, time-space windows for analysis (dx・dt = 0.42 A × 0.42 A × 0.42 A × 0.1 ps) (lapsed time after excitation t = 0.3 ps), 32 × 32 × 32 grid points, point-spread function radii 0.8 grid) (The oxygen atom in the first salvation layer (corresponding to the first peak) is omitted to make it easy to see.).

[Reference] T.Okamoto and M.Nagaoka, Chemical Physics Letters, 407, 444 (2005).